Программируемый микрокалькулятор Uniel US-54: «Игры разума»

- Цена: 658 ₽ (куплен за 475 ₽)
- Перейти в магазин
И снова здравствуйте, достопочтенные читатели. Сегодняшний мой обзор пройдёт под девизом «Я купил это за доллар!» Ну, положим, не за доллар, а за шесть, но всё равно на удивление дёшево. Героем же сегодняшнего обзора станет программируемый микрокалькулятор. И это не винтаж, десятилетия ожидавший своего часа в лавке антиквара, а современное и общедоступное электронное вычислительное устройство с качественной локализацией.
Те из вас, кто прожил достаточно долго, наверняка помнят такое некогда культовое явление, как программируемые микрокалькуляторы. Не удивлюсь даже, если у кого-то в своё время такой был, а может быть даже сохранился и до сих пор. Чаша сия не минула и меня: примерно полгода я имел возможность пользоваться довольно продвинутым по тем временам программируемым калькулятором «МК-61». Однако постичь все глубины его возможностей я так и не успел: случайный разряд статического электричества привёл к досрочному апгрейду.
И вот, увидев на «Озоне» программируемый калькулятор за немыслимые 475 рублей, я не поверил глазам своим и принялся искать подвох. А когда выяснилось, что никакого подвоха нет, сгрёб деньги в охапку и бросился покупать это чудо, пока кто-нибудь другой не сделал это прежде и вместо меня. И вот шесть дней спустя дрожащими от вожделения лапками я распаковываю свою новую прелесть.

Да-да, достопочтенный читатель, это и есть тот самый Uniel US-54, самый настоящий программируемый микрокалькулятор по цене коробки конфет. Что же я получил в обмен на скромную денежную сумму? А главное – зачем вообще человеку такое счастье?
Начнём с первого пункта. Итак, перед нами яркая глянцевая коробочка с изображением микрокалькулятора и живописанием его достоинств: двухстрочный дисплей, 279 функций, натуральная запись и – вот оно – «программирование»! Программируемых калькуляторов вживую я не видел уже очень и очень давно, и, кабы не эта строчка, покупка бы определённо не состоялась. Согласно надписи на коробке, предназначен сей калькулятор «для инженерных работников и студентов». Правда, «инженерные работники» с калькуляторами мне не встречались почти столько же лет, сколько и сами калькуляторы. А вот насчёт студентов – тут я готов поверить. Раздел инструкции про линейную регрессию немедленно пробудил воспоминания об университетских лабораторных по математической статистике и об очереди к единственному компьютеру, чтобы не закатывать Солнце вручную.
Кстати, об инструкции. Инструкция в коробке с калькулятором есть, занимает аж 96 листов и напечатана на двух языках, причём русскоязычная часть написана нормативным языком, не осквернённым гуглопереводом. Текст, в целом, достаточно подробен, чтобы разобраться во всех аспектах применения калькулятора, от арифметики до статистических расчётов. А ещё на первой же странице инструкции присутствует информация об изготовителе, и тут всё немного предсказуемо: калькулятор произведён в Китае.


Единственный недостаток руководства – размер шрифта. Если вы найдёте его слишком мелким, всегда можно скачать руководство от японского Casio fx-3950P, клоном которого Uniel US-54, собственно, и является.
Хоть калькулятор и адресован интеллектуально развитым слоям населения, изготовлен он отнюдь не из премиальных материалов. Электронно-вычислительная начинка заключена в пластиковый корпус тёмно-се… извиняюсь, цвета «Black Titanium».
Uniel US-54, вид спереди

Некоторые надписи над кнопками, особенно те, что нанесены красным цветом, на таком фоне читаются с трудом. Кнопки тоже пластиковые; цифровые – нормального размера, функциональные – приемлемого, а вот верхний ряд мелковат, их сподручнее нажимать ногтем. Весит калькулятор вместе с защитной крышкой немногим больше ста грамм, а ощущается ещё легче.

При этом его размеры составляют 160×84×18 миллиметров, что приблизительно соответствует габаритам смартфона с диагональю экрана 6,9 дюйма.
Питается устройство от двух батарей типа LR44 и, согласно инструкции, срок непрерывной работы от одного комплекта составляет 15000 часов. Индикатором разряда батарей калькулятор не оборудован, определять необходимость их замены предлагается по снижению контраста жидкокристаллического индикатора. Батареи спрятаны надёжно: чтобы их заменить, придётся открутить четыре винтика и снять заднюю крышку.
Uniel US-54, вид сзади

Также на тыльной стороне калькулятора присутствует логотип производителя, надпись «Made in China», бумажная наклейка с числами неизвестного смысла и назначения и небольшое отверстие с подписью «RESET», в глубине которого скрывается кнопка. Нажимать на неё нужно, если калькулятор наглухо «завис» (мне такого добиться пока не удавалось) либо сразу после замены батареек.
Калькулятор комплектуется пластиковой защитной крышкой, которая в «походном» состоянии защищает клавиатуру и экран, а в «рабочем» – прикрывает заднюю сторону калькулятора.

Крышка ощутимо люфтит и шатается, однако на своём месте держится. В руководстве особо отмечен момент, что крышку нельзя устанавливать «вверх ногами» во избежание поломки калькулятора.
Увидев на коробке надпись про «279 функций», на которые способен Uniel US-54, достопочтенный читатель наверняка подумал что-то вроде «Вот это мощь! Да мне за всю жизнь столько не использовать!». Жаль вас разочаровывать, но «функции» в калькуляторах совсем не таковы, как многие их себе представляют. Если подойти к вопросу с умом, окажется, что «ввести цифру 1» — вполне себе функция, а цифр на клавиатуре целых десять. Да что там, даже включение/выключение калькулятора тоже функция, причём важнейшая. А при творческом осмыслении – даже целых две.
Но всё равно список возможностей впечатляет: помимо арифметики, тригонометрии и логарифмических/показательных функций калькулятор умеет работать с натуральными дробями и комплексными числами, с угловыми мерами в двух разных форматах, понимает три системы счисления помимо десятичной, «знает» кое-что из комбинаторики, способен проводить статистические расчёты, выполнять регрессионный анализ нескольких видов, а также дифференцирование и интегрирование функций одной переменной численными методами.
А ещё он предоставляет в распоряжение пользователя семь ячеек памяти для хранения промежуточных результатов и 360 байт, в которых можно разместить до четырёх пользовательских программ на языке программирования, разработанном фирмой Casio и, как принято говорить в таких случаях, «не имеющем аналогов в мире».
Однако, несмотря на всё это изобилие, ряд простых, но очень нужных операций в калькуляторе почему-то отсутствует. Несколько позже я поведаю, чего мне не хватило для полного счастья и на какие ухищрения пришлось пойти, чтобы реализовать эту функциональность подручными средствами, а пока посмотрим, как воспользоваться тем, что есть.
Включить калькулятор несложно, кнопка «ON» расположена справа ниже дисплея. А вот выключить… Самый простой способ это сделать — заглянуть в инструкцию, и узнать, что сначала надо нажать «Shift», а потом — «AC». Кстати, если не нажимать никаких кнопок, примерно через 6 минут калькулятор выключится сам.
Первое, что бросается в глаза после включения калькулятора – непривычно двухстрочный экран. В нижней его части обычные семисегментные индикаторы, а вот сверху ЖК-матрица высотой в 8 пикселей с призывно мерцающим курсором.

Попробуем посчитать какое-нибудь несложное выражение. Например, наберём «2+2×2». Набранное на клавиатуре тут же отобразится в верхней строке. Кнопки «=» у Uniel US-54 нет; на привычном месте вместо неё находится клавиша «EXE». Если, руководствуясь интуицией (или знанием английского языка), её нажать, выяснится, что эта клавиша заставляет калькулятор вычислить введённое выражение и показать в нижней строке ответ: «6».
Простой советский, а также любой бухгалтерский и немало «научных» калькуляторов в такой же ситуации выдадут результат «8», что, очевидно, неправильно. Чуть более сложный «Калькулятор» из Windows 10 посчитает верно, однако если то же самое скормить «Калькулятору» в чуть ином виде – 2(2+2), программа вообще не поймёт, чего от неё хотят.
И вот тут будет уместно рассказать про «естественный ввод» арифметических выражений, по моему мнению, являющийся наиглавнейшим достоинством данного калькулятора. Суть его предельно проста: введите с клавиатуры математически корректное выражение, а с порядком выполнения действий калькулятор определится сам. Поверьте, он сможет.
Имеет естественный ввод и ещё одно не вполне очевидное применение. Возможность опускать лишние знаки умножения позволяет более компактно записывать математические выражения, что может быть актуально в режиме программирования. Например, выражение «2 tg 360D» на калькуляторе можно записать как «2 × tan (360 × D)», а можно – как «2 tan 360 D». В режиме программирования первый вариант займёт в памяти калькулятора 10 байт, второй – всего 6.
По примеру из предыдущего абзаца можно заметить, что тригонометрические функции здесь вводятся не так, как на «обычных» калькуляторах. Например, вычисление синуса 30° на большинстве калькуляторов выглядит так: набираем «30», нажимаем кнопку «sin» и получаем ответ. На Uniel US-54 нужно сначала нажать «sin», потом ввести число 30 и, наконец, нажать «EXE», чтобы в нижней строке появился результат. При этом в верхней строке вы будете видеть выражение, которое вы только что посчитали.
И не только видеть! Uniel US-54 запоминает некоторое количество последних вычислений с их результатами на случай, если вы захотите к ним вернуться, что-нибудь исправить и пересчитать заново. Перемещаться по «ленте расчётов» можно при помощи джойстика, расположенного под экраном калькулятора. Правда, история прошлых вычислений не безгранична, обычно памяти хватает на 4-6 строк, но обычно большего и не требуется.
Сверх того, калькулятор предоставляет довольно продвинутые возможности редактирования: помимо перемещения по тексту выражения он позволяет удалить символ под курсором, заменить неверно введённые символы и даже перейти в режим вставки и дописать недостающее в середину строки вместо того, чтобы набирать всё заново.
Впечатляет и возможность работать с угловыми мерами, представленными в градусах, минутах и секундах дуги. Допустим, мне понадобилось посчитать разность широт между Красноярском и Паттайей. Широта первого города – 56°00′43″, второго – 15°55′23″. Есть несколько способов сделать это с помощью обычного калькулятора, однако удобными их не назовёшь. А вот на Uniel US-54 для ввода углов в таком виде имеется специальная кнопка «° ❜ ❞», которую нужно нажимать после ввода градусов, минут и секунд. В нашем случае надо набрать
«56» «° ❜ ❞» «0» «° ❜ ❞» «43» «° ❜ ❞» «−» «15» «° ❜ ❞» «55» «° ❜ ❞» «23» «° ❜ ❞» «EXE»
и прочитать на экране ответ: 40°5′20″.

Некоторым недостатком можно считать то, что градусы, минуты и секунды на экране калькулятора отображаются одним и тем же символом — квадратиком сверху (в более продвинутых калькуляторах Casio вместо квадратиков отображаются символы градусов, минут и секунд). Если же вам нужны не минуты и секунды, а доли градуса, последовательность «Shift» «° ❜ ❞» выполнит преобразование угла из одного представления в другое.
Но что будет, если сделать на калькуляторе что-нибудь запретное? Например, разделить на ноль, извлечь квадратный корень из -64 или посчитать арксинус 10. Ничего страшного не случится: калькулятор не «зависнет», не отключится и не вызовет наряд Тьюринг-копов. Он в таких случаях просто выдаёт сообщение «Math ERROR». Впрочем, для любителей извлекать квадратные корни из чего попало есть режим расчётов в комплексных числах, где эта операция полностью корректна:

Ну а другую популярную ошибку, «Syntax ERROR», калькулятор выдаёт, если предложить ему посчитать математически некорректное выражение.
Есть две трубы…
Все вы, наверное, помните школьные задачки про две трубы, по которым что-то куда-то втекает и вытекает. На самом деле, конечно, задачи эти вообще не про трубы, а про операции с натуральными дробями, которые хоть и не сложны, но требуют внимания и усидчивости. Последний термин – эвфемизм, обозначающий способность к многократному повторению бессмысленных действий без внутреннего протеста. И вот как раз этой «усидчивости» у меня как не было, так и нет. А в детстве не было и калькулятора, который расправлялся бы с натуральными дробями столь же лихо, как обозреваемый.
Меня в своё время задачи про трубы неизменно погружали в тоску и уныние, поэтому сегодня у нас никаких труб не будет. А для демонстрации операций с натуральными дробями я выберу пример актуальный и жизненный: покажу, как вычислить крепость алкогольного коктейля.
Условием задачи пусть будет «Смерть после полудня» – ультимативно декадентский напиток, изобретение которого приписывается самому Эрнесту Хемингуэю. Канонический его рецепт выглядит следующим образом:
- Абсент: 40 мл
- Шампанское (брют): 100 мл
- Сахарный сироп: 10 мл
Сам я, когда готовил это зелье, на роль абсента выбрал относительно недорогой зелёный «Jacques Senaux» крепостью 60°. Шампанское подойдёт любое, тратиться на благородные сорта нет нужды. В моём случае под рукой оказалась 200-граммовая бутылочка какого-то итальянского игристого крепостью 10,5%, оно и пошло в дело. Ну а сахарный сироп я намешал собственноручно, взяв сахар из сахарницы, а воду – из чайника.
Типовой подход к решению такого рода задач предполагает, что сначала нужно посчитать объём спирта в каждом из ингредиентов, просуммировать их и разделить на общий объём получившейся смеси. С учётом того, что один алкогольный «градус» означает одну объёмную часть из ста, общее количество алкоголя в напитке составит 40(60/100) + 100(10,5/100) миллилитров.
Для ввода натуральных дробей в калькуляторе предусмотрена кнопка «а b/c», причём вводить с её помощью можно и правильные, и неправильные, и даже смешанные дроби. Первые два типа дробей вводятся очень просто: если мы хотим ввести дробь «4/5», нужно последовательно нажать «4» «a b/c» «5». На экране оно отобразится как
4⯾5
Смешанную дробь 2¾ ввести ненамного сложнее «2» «a b/c» «3» «a b/c» «4»; на экране в этом случае мы увидим
2⯾3⯾4
Более того, с дробями можно выполнять любые действия, как с обычными числами. При этом калькулятор старается держаться «натурально-дробной» нотации до последнего, однако если результат получается неудобоваримым, он всё же перейдёт на десятичные дроби. К примеру, если бы мы хотели умножить 2¾ на ⅘, сделать это можно было бы так:

Однако нам для решения задачи нужно посчитать выражение посложнее:
40(60⯾100)+100(10,5⯾100) «EXE»
Результатом будет 34,5: именно столько миллилитров чистого алкоголя содержится в нашем коктейле. И тут мы вспоминаем, что всё это нам теперь нужно разделить на полный объём, который составляет (40+100+10) миллилитров. Неужели, чтобы сделать всё правильно, придётся набирать выражение заново?!
К счастью, специально для таких случаев Uniel US-54 оборудован «устройством запоминания последнего результата» и кнопкой «Ans» (от английского «Answer» – «ответ»), позволяющей подставить в новый расчёт результат предыдущего. Так что набираем:
Ans ÷ (40 + 100 + 10) «EXE»
Результатом будет число 0,23 – именно такую долю занимает спирт в получившемся коктейле; чтобы перейти к привычным «градусам», её нужно умножить на 100. Однако существует способ получить результат сразу: вместо «EXE» нужно нажимать «%» («Shift» «EXE»), эта операция вычисляет, какой процент делимое число составляет от делителя. В этом случае на экране сразу появится требуемый ответ: «23».
Теперь название коктейля в дальнейших разъяснениях вряд ли нуждается: эффект от пары бокалов 23-градусного напитка с анисом, сахаром и волшебными углекислотными пузырьками превзойдёт все ваши ожидания.
Вычисляем коэффициент температурного расширения светлого времени суток в Красноярске
Прочитав заглавие раздела, половина достопочтенных читателей, ещё не забывших школьный курс физики, наверняка впала в ступор, пытаясь осмыслить прочитанное, другая половина нервно засмеялась, а третья – принялась шарить по столу в поисках чего-нибудь тяжёлого. Но не беспокойтесь, я не собираюсь шокировать почтенного читателя откровениями из альтернативной физики. Это всего лишь аллюзия на детскую загадку: «Отчего летом дни длиннее, а зимой – короче?»
Поскольку загадка – детская, то и ответ предполагается шуточный: «летом от жары день расширяется, а зимой от холода сжимается». Однако мы подойдём к вопросу со всей звериной серьёзностью: если день ведёт себя как физическое тело, стало быть, у него есть коэффициент температурного расширения. И, если набрать достаточно статистики, этот коэффициент можно вычислить!
За статистикой придётся прогуляться в интернет. Данные по среднемесячным температурам в Красноярске за последние 10 лет я взял с http://www.pogodaiklimat.ru/history/29570.htm, продолжительность дня – с https://timewek.ru/citysun.php?sID=24. Усреднив и то, и другое, я свёл результаты в следующую табличку:
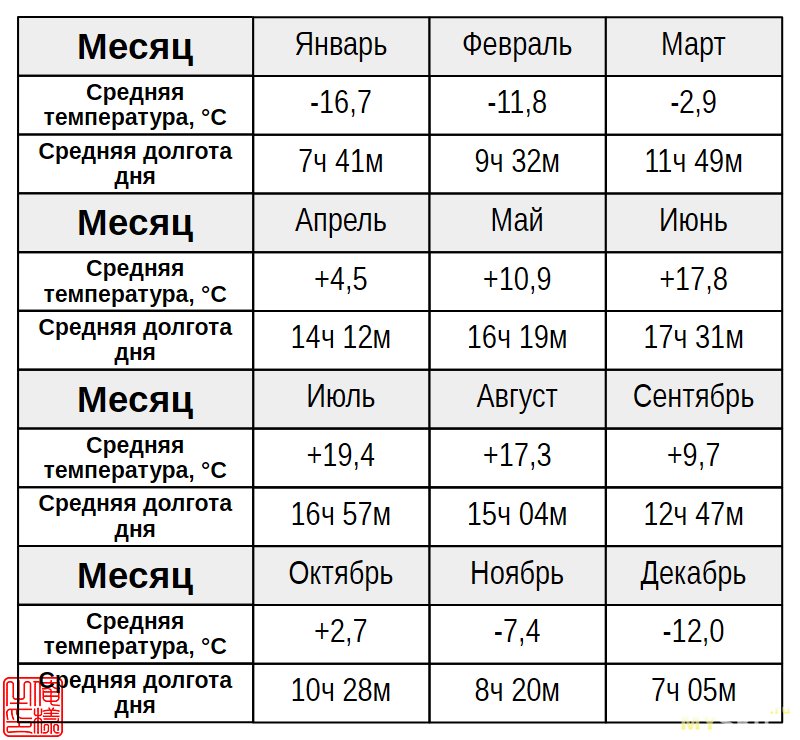
Исходные данные у нас теперь есть, что дальше? А дальше нужно посчитать линейную регрессию и определить параметры зависимости продолжительности дня от температуры.
Для тех, кто не знает, что это за зверь такой — «линейная регрессия», попробую объяснить вкратце. Допустим, мы предполагаем линейную зависимость некой величины Y от величины X. Точные параметры этой зависимости мы не знаем, однако имеем набор наблюдений, то есть пар точек (X₁, Y₁ ), (X₂, Y₂), (X₃, Y₃) и т. д. Наблюдения сделаны с некоторой погрешностью, поэтому просто взять и провести через все эти точки одну-единственную прямую не получится. Однако при помощи довольно утомительных вычислений можно рассчитать коэффициенты уравнения прямой, проходящей таким образом, что сумма среднеквадратичных отклонений реально зафиксированных значений от тех, которые «предсказывает» прямая, будет минимальна. Сведение набора наблюдательных данных к некой прямой, которая наилучшим образом их аппроксимирует, и есть та самая «линейная регрессия».
Все статистические расчёты Uniel US-54 выполняет в специально предназначенных для этого режимах. Режим вычисления линейной регрессии включается, если дважды нажать «MODE», затем — «2» (выбор режима регрессионного анализа) и, наконец, «1» (тип регрессии — линейный). После этого инструкция рекомендует очистить область статистических данных, нажав «Shift» «CLR» «1» «EXE».
Теперь можно приступать к вводу данных для анализа. Тут всё просто: вводим независимое значение, нажимаем клавишу «,», вводим зависимое значение, нажимаем «DT» (она же «M+»); на экране после этого появится надпись «n=1», означающая, что мы только что благополучно ввели первую пару значений.
Однако в качестве зависимого значения нам нужно вводить время, выраженное в часах и минутах. Что же делать? Можно при помощи всё того же калькулятора перевести эти значения в часы. Или в минуты. А можно пойти на небольшую хитрость: воспользоваться уже знакомой нам кнопкой «° ❜ ❞» и вводить время так, как будто это угловые меры. Почему так можно делать, предоставлю читателю догадаться самостоятельно. Так или иначе, чтобы ввести первое значение (-16,7°C, 7ч 41м), нужно набрать:
«(-)» «16.7» «,» «7» «° ❜ ❞» «41» «° ❜ ❞» «DT»
Второе и последующие значения вводим аналогично. Всё это калькулятор сохранит в области статистических данных; при помощи джойстика введённые значения можно пролистать и посмотреть, а при необходимости — исправить, удалить или добавить новые.
Когда данные будут введены, можно запросить параметры линейной регрессии A и B. Мы привыкли, что уравнение прямой описывается уравнением ax+b = 0, однако на родине калькуляторов Casio всё наоборот: японское уравнение прямой выглядит как A + Bx = 0. Чтобы получить первое из нужных значений, нажимаем «S-VAR» («Shift» «2»), дважды «вправо» на джойстике и цифру «2» («B») и «EXE». На экране появится:
B = 0,273553716
Это — коэффициент наклона прямой, и, одновременно, «коэффициент теплового расширения светлого времени суток», означающий, что повышение средней температуры на 1 градус увеличивает среднюю продолжительность дня на 0.2736 часа, или на 16 минут 25 секунд.
Схожим образом можно получить и второй коэффициент A, нужный для построения прямой; он равен 11,59442149. А ещё можно запросить коэффициент корреляции r, показывающий, насколько хорошо построенная прямая аппроксимирует экспериментальные данные. В нашем случае r = 0,93507198, и это очень хороший результат: коэффициенты корреляция выше 0,9 указывает на наличие сильной взаимосвязи между параметрами.
Положим, регрессию мы выполнили, что делать дальше? Всю эту хитрую математику изобрели не праздного любопытства ради (хотя, читая об иных научных достижениях, я начинаю в этом сомневаться): знание параметров аппроксимирующей функции позволяет ответить на ряд вполне обыденных вопросов. Например, «Когда включат/выключат отопление?» или «Какая будет среднесуточная температура в день равноденствия?»
У нас отопление включают, когда среднесуточная температура опускается ниже +8°C, а отключают — когда оно поднимается выше той же величины. Поскольку все коэффициенты зависимости продолжительности дня температуры калькулятору уже известны, можно вычислить, какая продолжительность дня соответствует заданной средней температуре. Для этого набираем: «8» «Shift» «S-VAR» «вправо» «вправо» «2» (на экране эта операция обозначена как «ŷ») «EXE», и на экране появляется ответ: 13.78 часа, которые тут же можно перевести в более привычные 13ч 47м. Приблизительно такая продолжительность дня в Красноярске бывает 3 сентября и 10 апреля. Если первая дата похожа на правду, то вторая отличается от реальности на месяц: отопление обычно включают в середине сентября и выключают во второй половине мая.
Можно выполнить и обратную операцию, то есть по известной продолжительности дня вычислить среднюю температуру. Возьмём продолжительность дня равной 12 часам; как вы можете помнить, равноденствие случается два раза в год, 22 марта и 22 сентября. Вводим «12» «Shift» «S-VAR» «вправо» «вправо» «1» (на экране калькулятора это символ «x̂»). Результат операции — 1.48°C. И вот опять: если для 22 марта это вполне реалистичное значение, то 22 сентября обычно гораздо теплее. Впрочем, странно было бы ожидать серьёзный результат от расчёта, изначально основанного на шутке.
Вайб-кодерам здесь не место
И вот мы подошли к ключевой особенности, выделяющей Uniel US-54 среди множества присутствующих на рынке инженерных калькуляторов: возможности самостоятельно создавать программы расчётов и исполнять их на микрокалькуляторе.
Несмотря на то, что его японские предшественники Casio fx-3650P и Casio fx-3950P начали выпускаться ещё в 2002-м, то есть более двадцати лет назад, следы жизнедеятельности их владельцев в интернете крайне малочисленны. Если у советских МК и американских HP была и своя фан-база, и некоторое число печатных источников, посвящённых их использованию, то изделия Casio и их клоны подобной популярностью похвастать не могут. Возможно, в японоязычном интернете дела обстоят иначе, но нам это вряд ли чем-то поможет. В общем, готовых реализаций даже широко известных алгоритмов, не говоря уже о различной экзотике, вы не найдёте.
Программируется Uniel US-54 на своём совершенно особенном языке программирования, более развитый (или менее урезанный?) диалект которого известен под названием «Casio BASIC». С привычным Бейсиком, впрочем, он имеет очень мало общего. В основе этого «птичьего языка» лежит всё та же естественная запись математических выражений, дополненная операторами для ввода значений ввода с клавиатуры, сравнения, условного выполнения команд, метками, переходами и командой останова для просмотра промежуточных результатов. В результате тексты программ для этого калькулятора получаются предельно плотными. Вот, к примеру, программа, по диаметру объектива телескопа, а также фокусному расстоянию объектива и окуляра вычисляющая его увеличение, разрешающую способность по критерию Рэлея и проницание по формуле Боуэна:
? → D : ? → X : ? → Y : X ÷ Y → M ◢ 140 ÷ D ◢ 2.5 ( 1 + log DМ )
Обратной стороной минимализма, однако, стал ограниченный выбор управляющих конструкций. Циклы? Подпрограммы? Сделай сам, если сможешь. И не забывай, что в твоём распоряжении всего 7 ячеек памяти, 10 меток на каждую программу и 360 байт – на все программы вместе. Да и «всех» программ, как оказалось, не может быть больше четырёх одновременно. Но они хотя бы не пропадают из памяти при выключении калькулятора.
Самое неудобное в режиме программирования — то, что программа целиком выводится в одну строку, по которой можно перемещаться влево-вправо при помощи джойстика. Разумеется, есть режимы вставки и замены, и удаление символов, но когда из начала программы нужно перейти в конец, единственный способ — зажать джойстик и ждать, пока курсор доползёт в нужное место. А ещё калькулятор поощряет идеи open source: единственный способ обмена программным обеспечением с внешним миром – вручную переписать текст программы и так же вручную набрать его с клавиатуры.
Разобравшись в основах, я попытался выйти за границы и нарушить правила, соорудив конструкцию «Goto X». Увы, на попытку перехода к метке с вычисляемым номером калькулятор отреагировал сообщением «Syntax ERROR». Не нашли понимания у калькулятора и некоторые другие радикальные идеи. Однако кое-что всё же удалось. В частности – написать кусок кода, выполнявший отсутствующую операцию взятия целой части (правда, только для неотрицательных чисел, но мне и такой было достаточно). Для числа, хранящегося в ячейке памяти A, соответствующий код умещается в 13 байт:
Fix 0 : A : Rnd : Ans – ( Ans > A ) → A
Если же нужное значение находится в ячейке M, за счёт использования операции «M–» можно сэкономить ещё три байта.
Полагаю, после слов «сэкономить три байта» любители стильных-модных-молодёжных языков программирования приуныли. Кто-то даже мог подумать, что на этом и вовсе невозможно запрограммировать ничего сложнее программы решения квадратных уравнений. Поэтому в следующем разделе сего обзора я изо всех сил постараюсь продемонстрировать, что это не так.
Флоучартинг унд мракобесинг
Возможно, вы находите перспективу, обозначенную в заглавии раздела, несколько сомнительной, однако позвольте вас заверить: здесь вам не грозит погрязнуть в предсказаниях Ванги или столкнуться с заблудившемся в коридоре затмений ретроградным Меркурием. Пристегните ремни, мы отправляемся на увлекательное сафари в дебри отборной поп-трэш-духовности!
Однако прежде — совершенно необходимое медицинское предупреждение:
Если вы страдаете трискайдекафобией, возможно, вам сто́ит воздержаться от чтения нижеследующего текста, ибо в нём будет многажды упомянуто это число.
Конечно, было бы занимательно написать программу для расчёта дней шестидневной недели «рокуё», без которой совершенно невозможно представить мир современных японских суеверий. Однако стоящая за японским лунно-солнечным календарём математика настолько громоздка, что адаптировать её к возможностям Uniel US-54 было нереально. Поэтому я взялся за менее амбициозную календарную задачу: запрограммировать расчёт всех пятниц, приходящиеся на 13-е число, начиная с заданного года и месяца. Кстати, генеральным спонсором программы согласился выступить Джейсон Вурхиз.
Вообще день недели на произвольную дату григорианского календаря вычисляется по широко известной в узких кругах формуле Зеллера. Вариант этой формулы, адаптированный для целочисленных расчётов, выглядит так:
W = (D+〚13(M+1)/5〛+Y+〚Y/4〛−〚Y/100〛+〚Y/400〛) mod 7
В этой формуле символы 〚〛 означают взятие целой части числа, D – номер дня в месяце, mod — остаток от деления, а результат W — день недели. Причём дни недели по Зеллеру нумеруются несколько неожиданным образом: 0 — суббота, 1 — воскресенье, 2 — понедельник, ну и так далее.
Другая особенность формулы Зеллера в том, что коэффициенты M и Y – «модифицированные» номер месяца и года. От обычных они отличаются тем, что для января и февраля к номеру месяца нужно прибавить 12, а от номера года отнять единицу. Ограничив область допустимых дат 13-м числом месяца, а также 20-м и 21-м веком, формулу можно сильно упростить. А ещё по некоторой причине, которую я назову позже, было бы удобно, чтобы пятнице соответствовало W, равное нулю, а не шести. Поразмыслив над формулой, я вывел такой вариант проверки «приходится ли 13-число в таком-то месяце такого-то года на пятницу»:
(〚13(M+1)/5〛+〚5Y/4〛 − 1 ) mod 7 = 0
Выражение выглядит настолько простым, что кажется: введи его в калькулятор, и программа тут же заработает. Так бы оно и случилось, если бы не отмеченный выше нюанс с выделением целой части числа. Когда нужный кусок кода уже кем-то написан, всё выглядит простым и понятным, однако прежде, чем это случилось, мне пришлось предпринять небольшое исследование команды Rnd и особенностей её работы.
В комплектной инструкции о ней не сказано почти ничего, а то, что сказано, не соответствует действительности. Соответствующий раздел документации вообще выглядит так, как будто его забросили, едва начав писать. Неудивительно, что на «Озоне» в отзывах о калькуляторе я обнаружил жалобу на то, что округление «не работает».
Потратив с полчаса на эксперименты, я выяснил: Rnd вполне работоспособна, но лишь в режиме «Fix N», где она округляет числа до N-го знака после запятой. Однако просто взять и увидеть результат работы этой функции на экране не получится, поскольку в Fix-режимах результат отображается на экране и без того округлённым (что, однако, не затрагивает его внутреннее представление, хранимое в регистре Ans). После такого открытия реализация недостающих команд становилась задачей не просто разрешимой, но даже не особо сложной.
Однако код вычисления остатка от деления был бы достаточно громоздким. В отличие от проверки «является ли число целым», которую реализовать куда проще: если после округления число не изменилось, значит, дробной части у него нет. Так что теперь вы знаете причину, по которой я добивался, чтобы отсутствие остатка от деления означало пятницу.
Известно, что древние люди не садились за программирование, не совершив перед этим ритуал, известный под именем «флоучартинг». Вооружившись карандашом и терпением, они вычерчивали на листе бумаги блок-схему (то бишь «flow chart») будущей программы. Чем точнее и подробнее была блок-схема, тем легче было по ней написать программу и тем надёжнее она работала. Так людям древности удалось слетать в космос, высадиться на Луну и совершить много других удивительных деяний.
Однако шли годы, люди обленились и возгордились, забросили освящённые веками духовные практики и, в конце концов, провозгласили, что «настоящие программисты не флоучартят». Вселенная такое не простила. Оттого ныне, чтобы вы могли просто прочесть этот текст, ваш браузер должен пожрать десятки и сотни мегабайт памяти, а на Луну больше не летает никто.
Но знаете, вычислительные алгоритмы, что бы они ни вычисляли, и программируемые микрокалькуляторы, что бы на них ни программировали — превосходная возможность вернуться к истокам. Так что я нашёл в шкафу лист бумаги в клеточку и со второй попытки изобразил на нём рабочую блок-схему. Вот такую:
«Пятницы, 13-е». Блок-схема.
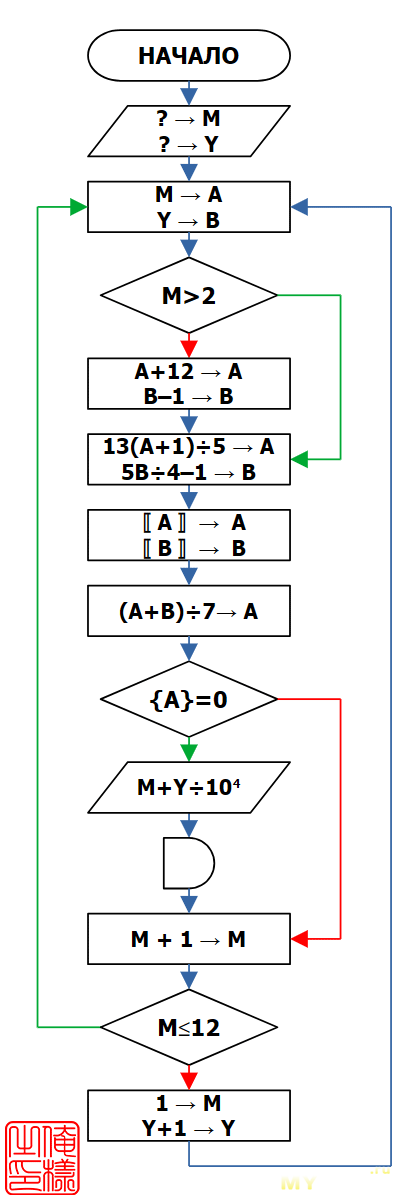
Поскольку представленный на блок-схеме алгоритм предстояло перевести на язык команд калькулятора, я изначально придерживался нотации, максимально приближенной к калькуляторной. Впрочем, блок-схема настолько проста для понимания, что по ней не составит труда воспроизвести эту логику на любом другом языке программирования, лишь бы в нём присутствовал ненавистный Дейкстре оператор GOTO.
В моём исполнении текст программы, для вящего удобства понимания разбитый на строки и уснащённый отступами, вышел таким:
? → M :
? → Y :
Lbl 0:
3 > M → C :
M + 12 C → A : Y – C → B :
2.6 A + 2.6 → A :
5 B ÷ 4 – 1 → B :
Fix 0:
A : Rnd : Ans – ( Ans > A ) → A :
B : Rnd : Ans – ( Ans > B ) → B :
( A + B ) ÷ 7 → A : Rnd : Ans ≠ A ⇒ Goto 1 :
Fix 4:
M + Y ÷ 10ˣ 4 ◢
Lbl 1:
1 M+ :
12 ≥ M ⇒ Goto 0 :
1 → M : Y + 1 → Y :
Goto 0
Объём получившейся программы составил 135 байт, причём в них уместился даже вывод результата в формате «месяц.год». Концепция, лежащая в основе форматирования вывода, проста до крайности: если номер года разделить на 10000 (или, что то же самое, но чуть короче, на 10⁴) и к результату прибавить номер месяца, получится почти то, что нужно. А чтобы получилось в точности то, что нужно, необходимо включить режим округления до 4 цифр после запятой (и не забыть его выключить после того, как вы завершите работу с программой).
А теперь — момент истины. Запускаем программу, на запрос «?→M» вводим «11», а на «?→Y» отвечаем «2025». Это значит, что мы хотим искать пятницы, 13-е начиная с ноября 2025-го года. Нажимаем «EXE», калькулятор на мгновение задумывается и выдаёт ответ «2.2026», что означает: следующая пятница, 13-е настанет в феврале 2026-го. Смотрим календарь на следующий год — так и есть.
Раз за разом нажимаем «EXE», и получаем: 3.2026, 11.2026, 8.2027, 10.2028, 4.2029, 7.2029, 9.2030 и так далее. Проверяем по календарю — программа не ошиблась!
С первой задачкой мы справились блестяще. Теперь давайте попробуем залудить на калькуляторе алгоритм посложнее. Например, построить знаменитый «Квадрат Пифагора». Ну, ныне, может, и не столь знаменитый, однако в 90-е он был знаком всякому купившему в вокзальном ларьке газету с названием то ли «Оракул», то ли «Тайная власть» и, в ожидании автобуса, прочитавшему её «от корки до корки».
В качестве исходных данных для расчёта возьмём дату 25.10.1917. Перво-наперво необходимо изобразить антуражный квадрат и пронумеровать его ячейки цифрами от одного до девяти.
Пустой «Квадрат Пифагора»
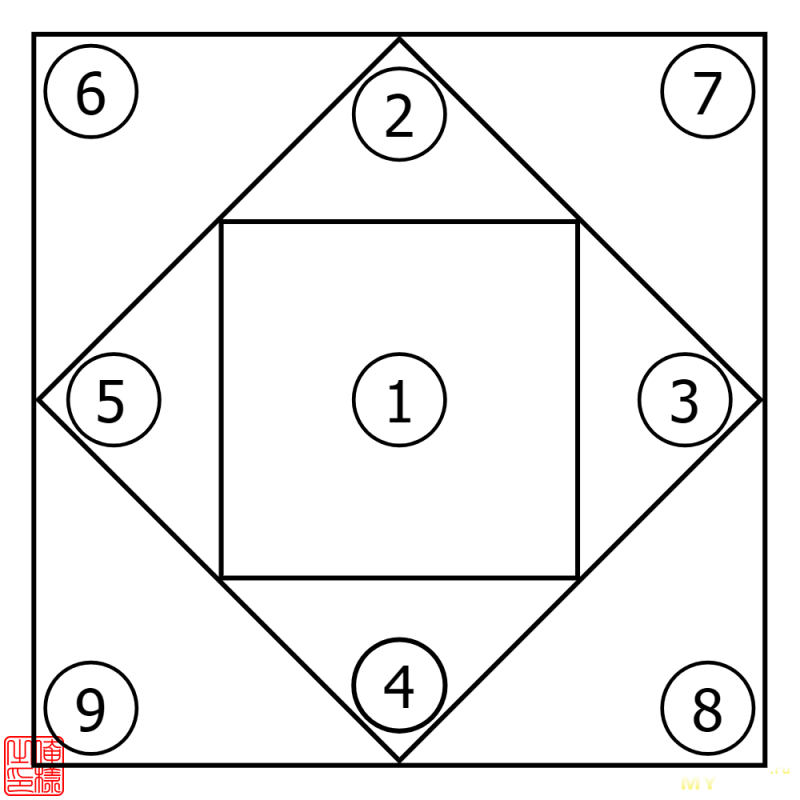
Затем все цифры интересующей нас даты выпишем в ряд (нули можно выбросить, ибо они ни на что не влияют): «25101917». Далее эти цифры полагалось сложить и получить второе число (в нашем случае результатом будет «26»). Процесс сложения цифр повторялся до тех пор, пока сумма не становилась однозначной; здесь это случится на третьем шаге, когда «2» и «6» дадут в сумме «8». И, наконец, в соответствующие ячейки квадрата нужно было поставить столько плюсиков, сколько раз соответствующая цифра появилась по ходу вычислений.
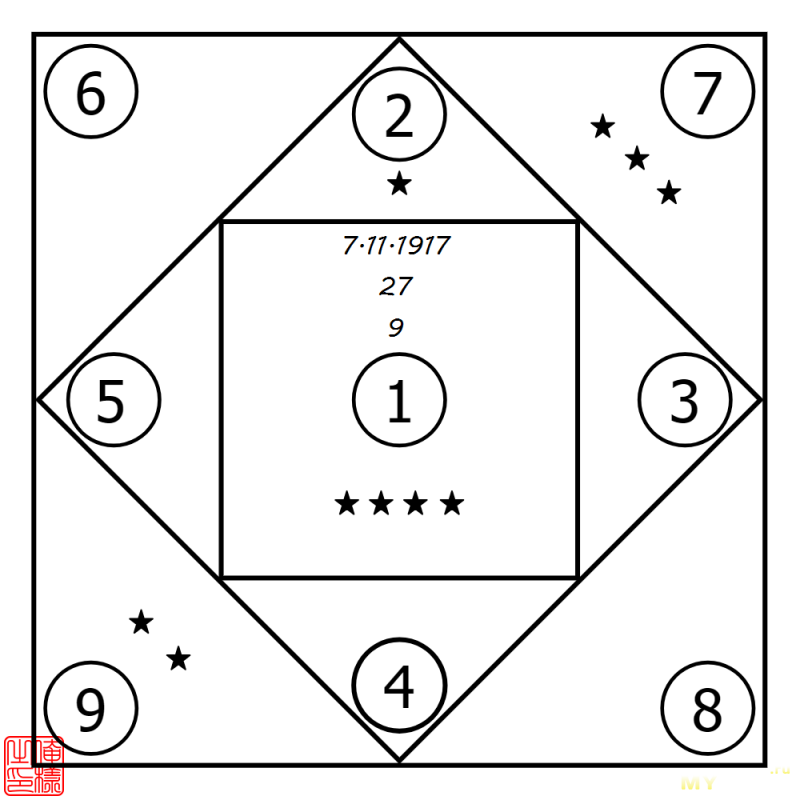
«Квадрат Пифагора» для даты 25.10.1917
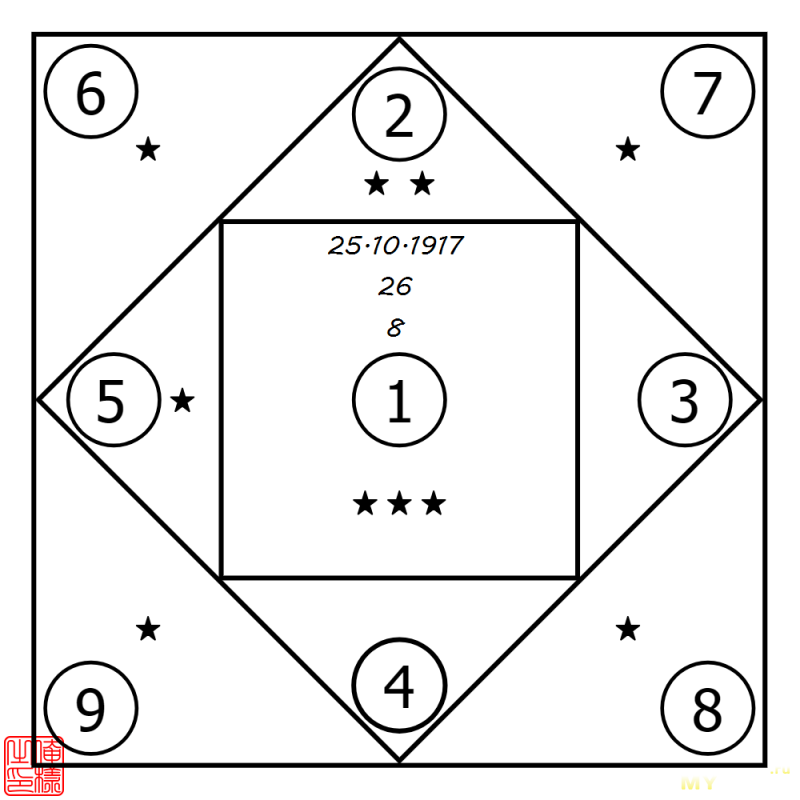
Финалом всей этой низшей математики было толкование полученной фигуры на основе числа плюсиков в каждой из ячеек квадрата. Какая цифра что означала, за давностью лет я уже не помню, но это и несущественно. Как несущественно и то, каким образом за полтысячи лет до нашей эры Пифагор исхитрился изобрести гадательную систему на основе позиционной системы счисления (впервые встречающейся в письменных источниках 5 века н.э.) и оперирующую положительными датами «от Рождества Христова».
На любом «серьёзном» языке программирования такая программа пишется минут за десять, не приходя в сознание. Однако реально ли втиснуть сию последовательность арифметических махинаций в ограниченные возможности микрокалькулятора?
У меня получилось. Начал я, опять же, с рисования детальной блок-схемы…
«Квадрат Пифагора». Блок-схема.
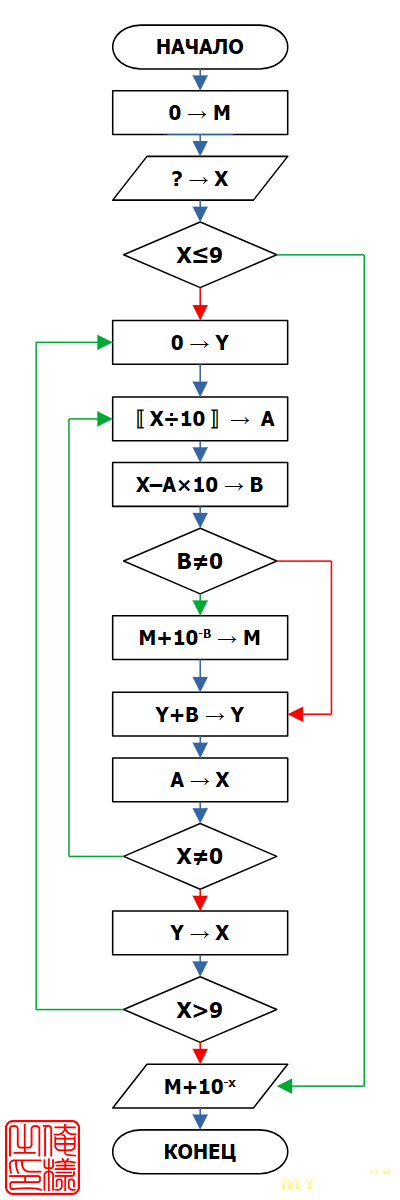
…которую потом оставалось лишь «развернуть» в текст программы.
0 → M :
? → X :
9 ≥ X ⇒ Goto 2 :
Fix 0 :
Lbl 0 :
0 → Y :
Lbl 1 :
X ÷ 10 → A : Rnd : Ans – ( Ans > A ) → A :
X – 10 A → B :
B ≠ 0 ⇒ 10ˣ ( –B ) M+ :
Y + B → Y :
A → X :
X ≠ 0 ⇒ Goto 1 :
Y → X ◢
X > 9 ⇒ Goto 0 :
Lbl2 :
Norm 2 :
10ˣ ( –X ) + M
Здесь на всё про всё хватило 105 байт. А, исключив из рассмотрения вырожденный случай с числом из одной цифры, программу можно было сделать ещё на 9 байт короче.
Пользоваться программой просто до крайности. Запускаем, на вопрос «X?» набираем все цифры даты («25101917»), жмём «EXE» и, мгновение спустя, получаем результат сложения всех цифр: «26». Опять «EXE», и на экране очередной результат сложения: «8». И, наконец, после ещё одного «EXE» получаем окончательный ответ: «0.320011111». Расшифровать его не составит ни малейшего труда: в первом разряде после запятой будет количество единиц в «квадрате Пифагора», во втором — количество двоек, в третьем — троек, и т. д. Можете сравнить с приведённым выше «квадратом», посчитанным вручную — совпадение будет полным.
На этом я завершу электронно-вычислительную часть сегодняшнего повествования, а на десерт поведаю достопочтенному читателю пару леденящих кровь и в высшей степени правдивых историй, которые вы не найдёте ни в одном гугле.
Первая из них самым непосредственным образом касается как самого «Квадрата Пифагора», так и даты, выбранной мною для его демонстрации. Повествует эта история о произошедших в Петрограде событиях более, чем столетней давности.
Как вы, может быть, помните, в октябре 1917 года там случилась революция, в дальнейшем получившая название Великой Октябрьской Социалистической. Несмотря на достигнутый «в моменте» успех, революционеры со всей отчётливостью осознавали шаткость своего положения. А потому хватались буквально за любую возможность это положение упрочить, прибегая, помимо всего прочего, к практикам, весьма далёким от декларируемой философии материализма. В частности, красные числогадатели раскидали дату революции на «Квадрат Пифагора» примерно так же, как это сделал я несколькими абзацами выше. Программируемых калькуляторов тогда ещё не изобрели, однако они как-то справились. И, согласно всем расчётам, «квадрат» выходил слабый и вялый, предрекая делу революции скорую и бесславную кончину.
Казалось бы, поезд ушёл, и с этим уже ничего не поделать. Не исполнять же, в самом деле, взятие Зимнего «на бис» в нумерологически благоприятную дату. И тут кого-то осенило, что, если пересчитать дату революции с юлианского календаря на григорианский, числовое наполнение «квадрата» изменится, суля радикально иное и куда более многообещающее будущее.
И ради этого сменили календарь?!
Воспрянув духом от такого известия, большевики ударными темпами провели календарную реформу, не смутившись даже тем, что октябрьскую революцию по «новому стилю» предстояло праздновать в ноябре.
Другая история относится уже ко временам Второй Мировой. То, что среди высшего руководства нацистской Германии хватало приверженцев всяческой мистики вообще, и астрологии в частности, давно ни для кого не секрет. Печатная, а ныне и интернет-пресса разной степени желтизны порасскажет вам на эту тему всякого, много и охотно, начиная с такого, что вполне могло иметь место в реальности, и заканчивая психоделическим «тёмным фэнтези». Сколько правды в тех рассказах, решайте сами, однако стоило про оккультные увлечения нацистской верхушки прознать британской разведке, как в Лондоне поспешили собрать собственное астрологическое подразделение. Только вот вовсе не духовные прозрения и предсказания будущего интересовали британскую разведку. Команда английских звездочётов выступала в роли приглашённых экспертов, а их задачей было воспроизвести советы, что шептали на ухо Гитлеру их берлинские коллеги, глядя в свои гороскопы.
Какая из всего вышеизложенного следует мораль? Я бы сказал, разнообразная. Кто-то, подобно Пифагору, может увериться, что числа и правда правят миром. А кто-то, наблюдая череду «совпадений» и «предсказаний», задастся вопросом, что здесь первично: тайное могущество чисел, или всё же люди, что сверяют каждый свой шаг с нумерологическими расчётами?
Однако давайте, наконец, выйдем из астрала и подведём итоги всему, что было сказано касательно обозреваемого микрокалькулятора. В целом об Uniel US-54 я составил самое положительное мнение. Считать что-нибудь по мелочам мне приходится достаточно часто, поэтому держать на столе отдельное и всегда готовое к работе устройство с физическими кнопками оказалось удобнее, чем запускать «Калькулятор» Windows или разблокировать мобильник и искать в нём нужное приложение. Автоматизация повторяющихся расчётов при помощи программ востребована реже, но тоже находит применение. Не говоря уже о том, что программирование на этом калькуляторе со всеми его ограничениями и неочевидными возможностями можно рассматривать не только как практическую дисциплину, но и в качестве вычурной математической головоломки.
Покупать или нет? Это, конечно, дело глубоко личное и где-то даже интимное, однако я вижу лишь два серьёзных аргумента «против». Uniel US-54 вам не нужен, если вы не можете припомнить, когда в последний раз пользовались хоть каким-то калькулятором, либо у вас уже есть микрокалькулятор лучше, чем обозреваемый.
В остальном же он успешно справляется как с бытовыми расчётами, так и с вычислениями в рамках школьной программы, а также может пригодиться студенту не слишком математического ВУЗа. И, конечно же, это просто подарок любителям ретропрограммирования и обширный полигон для «игр разума».
Достоинства
- Достаточно подробное руководство на русском языке
- Естественная запись математических выражений
- Широкий набор функций, достаточный для бытовых и учебных целей
- Возможность программирования
- Цена
Недостатки
- Не самая удачная цветовая гамма
- Очень мелкие символы режимов работы калькулятора на экране
- Ограниченный набор управляющих конструкций во встроенном языке программирования
- Отсутствуют функции взятия целой или дробной части числа а также остатка от деления
- Невозможность сохранения набранных программ на внешнем носителе
- Нельзя использовать на ЕГЭ
| +267 |
24269
76
|
| +57 |
2380
112
|
| +81 |
3642
119
|
замечу, что за аналогичную сумму можно раздобыть куда более интересный девайс (правда, не «программируемый»), клон одноименного casio:
Программируемые — нельзя.
У исходника (casio, который за 900р. в ДНСе раньше был, нынче — хз) на упаковке это было со всех сторон написано. что можно на егэ и по ссылке была скан официальной пдфки с разрешением, который можно предъявить, чтобы не отобрали.
Подобные же приключения испытаны геодезическими сигналами в Студгородке и на Дрокинской горе (там вообще воздвигли достойное Церетелли убожество).
Это-то как раз самое интересное. Помню, в 90-е Красноярску обещали светлое будущее оккультной столицы России с ауграмами.
А где оно там? Ни разу на глаза не попадалось.
О, да! Реально расцветала махровая дикость.
На западном углу обрыва. Вполне могли снести сам сигнал и воздвигнуть очередной крест.
сохранился?
В эпоху смартов, конечно, все это выглдяит как рудимент, хотя вон он, на столе лежит, еще с института, купленный в киоске «все по 3» в 90х еще, все еще работает ) но пользуюсь очень редко.
P.S. Долго искал под винду/линь хороший и мощный калькулятор, оставновился на этом
Считает даты, время, дроби, градусы, и по моему даже римские числа.
А главное, при должной настройке, выглядит просто как поле ввода на экране и не занимает места вовсе.
Таскаю его по всем компам за собой уже лет 20… На 11 вполне себе работает, по комбинации кнопок (не NumLock конечно, как когда-то было задумано автором) успешно вызывается…
А так, сейчас модно прямо в PowerShell считать. Думаю и Линукс тоже с подсчетом в терминале может справиться.
таблица умножения с тех пор не изменилась.
Пользуюсь непрерывно с 2003 года.
Даже если тут тоже можно сыграть в «посадку на луну» то уже не тот эффект…
Хотя товар уже давно не нужен, но обзор зачетный!
Так что может оно и имеет ограниченный но стабильный рынок.
например из современного: модели Casio CG10, Casio CG50, Casio CG100 (в прошлом году вышел), вся линейка Ti nSpire, HP Prime.
Я закончил школу в 77, а первый раз калькулятор в руки взял в следующем. Их просто не было в продаже.
Но уже в середине 80-х приходилось ремонтировать школьные калькуляторы.
Кстати, программируемый офисный калькулятор «Искра-124» был выпущен только в 79 году.
Так что не согласен с
Я тогда впервые в магазине в Нежине возле вокзала увидел Б3-09М за 90р.
Возвращался из Полтавы, когда не поступил в военное училище. А уже в 81 мы такой калькулятор приспособили как счетчик оборотов в курсовой работе.
Но в середине 80-х калькуляторы были — только простенький девайс стоил 25 рублей. А более сложных до середины 90-х не видел, а там уже купил МК-61 (по советской вроде как цене, а там уже заодно и спектрум купил, и до первого 386 оставалось недолго).
По сравнению со спектрумом, Интел до 300-400 мгц был скучный.
Лично мне вместо спектрума прекрасно зашёл 8086 с ms dos 3.30.
Даже CGA был круче спектрума по графике, а уж выбор ПО — спектрум близко не валялся.
А когда собрал 486 и поставил 3.11 — можно было реально делать многое.
Куда там убожеству спектруму.
Может, все зависить от возможностей? На работе у меня всегда был выбор техники. Начиная с ДВК-2 и Yamaha MSX
Дома самодельный львов и несколько десятков дискет с играми. Большинство из которых я сам перегонял с кассет.
Когда мне достался Правец-16 с неисправным ST-225 я восстановил, поигрался месяц и не жалея продал. Ну не нужен он дома. Даже с модемом.
Хотя несколько игрушек для своего Спектрума я скачивал с какой-то Ленинградской BBS.
А если сравнивать с 8086, то всё очень даже не так однозначно.
5 миллионов копий — это не так уж мало. При этом, мне кажется, сюда не входят многочисленные его клоны.
Была еще полезная книжка М. О'Рурка «Таблицы умножения», выдержавшая много изданий в СССР, я тоже ей пользовался, реально экономила время до калькуляторов
Может, в совсем древние времена. А так — меньше одной инженерской зарплаты. В отличие от компьютеров, которые стоили как цветной телевизор (абсолютно культовый предмет).
А первый 286-й у нас в лаборатории стоил, как зерноуборочный комбайн, если в рублях.
Например, посадка космического корабля на Луну.
Батарейки вот только жрал…
Только мало кто его в глаза видел.
Сейчас даже фоток не найти…
Принтер по-моему стоил каких-то невменяемых денег, что его даже не пытались найти.
Были Блоки Расширения Памяти (БРП). В некоторые из них можно было записывать свой код программы. Собственная память была не такая уж и емкая. Поэтому ценность модуля с магнитофоном была под вопросом. К тому же уже подходило время Спектрумов. И возиться с записью на магнитофон для калькулятора и для Спектрума было существенной разницей по результату…
Собственной памяти в МК52 вроде было под 500 байт, т.е. несколько своих туда лезли.
В собственную память больше 3х программ почему-то забить не получалось. Видимо программы были слишком большими.
Была игрушка, в которой переключатель град-рад использовалась в качестве джойстика для управления самолетом. Последовательно показывалась высота полета самолета, высота гора, которую надо облететь, и еще что-то. Была очень тяжелая для хранения в памяти… Навскидку обработка джойстика 50-60 байт занимала. Память была плюсом в отличии от того же МК-61, в котором после выключения стиралось из памяти вообще все.
там при правильном подборе аргумента одной тригонометрической функцией обходилось. А дальше два ветвления по знаку…
(сам игрушки писал с управлением по Р-ГРД-Г… Что то типа слалома… но то давно было, лет 35 назад)
На компе много лет DreamCalc DC, тоже casio-подобный калькулятор.
56°00′43″
-15°55′23″
(56-1-15)°(00+60-55)'(43-23)"
Я понимаю ещё длину по поверхности по координатам посчитать, но разницу…
Вот мой трудяга, до сих пор живой с 97 года
такой же как у вас ситизен также имеется в моей скромной коллекции.
он, кстати, программируемый, процесс похож на тот, что описан в топике выше.
Он программируемый, я на нем в институте каие-то лабы или курсачи половине группы пересчитал. Одна программа, ввод значений, и только списывай ответы.
Но как и что там считалось… хоть убей не помню.
Тут-ностальгия.
Побольше таких обзоров!
Пы.сы. я бы еще про логарифмическую линейку краткий курс послушал.
интересно будет почитать.
Особенно в магазинах, где в одном килограмме то 900, то 800г. Одним движением пересчитывается цена нормального (метрического) килограмма )))
Да и корни квадратные, синусы малых углов
можно посчитать по-быстрому.
Линейка на безеле
Как вижу, это его наследник. Любопытно…
Как вижу, это его наследник. Любопытно…
P.S. Ну, и как в подобной компании не припомнить Виталия Светославовича Луговского? :-)
Современные процессоры, что в компах, что в смартфонах — работают так же, но это на нижнем уровне.
На Ява-скрипте можно сделать локальную html-страничку, открыть в браузере и решать любые задачи.
Шуриков тоже 3. Электроотвертки доставались разными путями но на кадмиевых аккумах кривые и не используемые. Одна покупалась ради биты квадрат 2х2 мм. Другая была выдана матери каким-то бонусом и перепала мне. Подумываю о покупке нормальной но пока не очень актуально
Но это про фейки, были ещё так я уже и не вспомню.
Вспомнил студенчество)
Только солнечные панели подводили, напрочь игнорировали люминисцентные лампы класса. :(
А так и натуральные дроби, и всякие градусы, радианы, и скобки и тригонометрия.
Я в итоге наколхозил батарейку параллельно батареям через диод, на разъеме из наконечников от стержней шариковых ручек (как вспомню, так вздрогну. :) ). Но оно даже работало.
Ну или старался садится ближе к окнам.
Да и сложно тогда было, в целом, с калькуляторами.
А ещё были часы с калькулятором. Но по факту пользоваться тоже не очень. В кнопки пальцем не попадал, а спички с собой обычно не было.
МК71 слизывали с Casio FX-950 и весь функционал хорошо реализовался, кроме солнечной панели.
уже лет семь ищу этот FX-950 на ибее и все никак не удается найти, редкий, а значит дорогой.
МК51 предположительно слизывали с Casio fx-2500, если кому интересно.
собственно — МК71 был наверное единственным вариантом для натуральных дробей. У меня был еще и МК60 (простой калькулятор на солнечных батареях) — он работал гораздо лучше (потребление меньше, хотя и площадь батареи тоже меньше). Где он сейчас — не знаю. где то у бабушки был, а потом после смерти — наследство делили без меня… А вот МК71 у меня валяются две штуки… Один мой. А второй — приданное жены. Как оказалось — у нас с ней одинаковые вкусы на хорошие вещи. :)
за мк-71 отдал зарплату 1,5 месяца работы в стройотряде
совсем не жалел, очень помогал!
А 71 и включается, и считает, и даже в родном чехольчике. Но у кнопок — так себе состояние, и переключатель градусы-радианы разболтан.
Sharp EL-W516 — мой настольный
менять значения и пересчитывать,
если нужен расчет с условиями и переходами,
если EXEL громоздок и запутан…
и если нет желания )) покупать физический программируемый калькулятор с программированием которого потом нужно разбираться, то…
в общем, порекомендую две программы, которыми периодически пользуюсь на работе и дома:
это Чиста Калькулятор (v2.0) freesoft.ru/windows/chista_kalkulyator — привожу одну из доступных ссылок, т.к., к сожалению, автор его забросил, но, имхо, он самый удобный из подобных программ и я им пользуюсь уже более 15 лет — это мастхэв для всех «счетоводов» )))
и это SpeedCrunch heldercorreia.bitbucket.io/speedcrunch/download.html много встроенных полезняшек, но «ЧК» всё равно мой фаворит)))
п.с. да, эксел и его бесплатные друзья из всяких опен/либре/впс и прочих офисов круче и функциональней, но реальность такова, что чаще гораздо быстрее, удобнее и понятнее визуально посчитать в ЧК.
п.п.с. МК-61 и БЗ-36 наше всё, но ЧК дает им фору в стотыщмильёнов процентов )))
Оказывается, столько людей, которые находят применение и, главное, пользуются! в быту калькулятором, понимая то, что они делают и для чего.
Даже завидую :)
Когда в 87 году на лабораторной работе достал логарифмическую линейку- препод чуть не прослезился)) Пять баллов получил легко!
Ну или Наука и жизнь, но скорее первое.
Советским пятиклассникам об этом в главе «Молекулярное строение вещества» в учебнике физики (чтобы хоть кого-то спасти от обвинений в краже при разведении спирта?) сообщали в начале учебного года.
Менделеев как раз над этим и трудился, где вы ошиблись.
Я и сейчас проверяю работу новой схемы на макетной плате, их китайцы наделали разных размеров отличного качества, а если нужен один экземпляр, то так и оставляю, но разводку делаю на компе.
По нынешним временам аппарат малополезный, это и так ясно, но по меньшей мере прикольный.
И комментарии.
Оказывается мы есть, которые пользуются калькуляторами)))
Началось с 83 года. Б3-34. В институте был незаменим.
И стало как болезнь. Коллекция из почти трёх десятков калькуляторов.
С жемчужинами)
Нет дополнительного двухкомпонентного лака на кнопках и на надписых на корпусе.
Это проблема дешовых калькуляторов.